Miremos el primer caso de factoreo, y supongamos que quiero hallar la superficie del siguiente rectángulo:

Ésto lo puedo hacer de dos maneras distintas, por un lado, sumar las superficies de los dos rectángulos que forman parte del rectángulo mayor, o también, sacar directamente la superficie del cuadrado mayor, sumando las medidas de las bases de los dos rectángulos que lo conforman. Como ambas formas de obtener la superficie, es lo mismo, entonces, las expresiones que representan esa superficie también lo serán.
Vamos por ejemplo al tercer caso: lo que se suele llamar trinomio cuadrado perfecto, que no es otra cosa que, el desarrollo de un binomio elevado al cuadrado. (se acuerdan que la potenciación no es distritubitva con respecto a la suma y a la resta??, bueno, aquí tienen la forma de resolverlo). Veámoslo geométricamente

Hallar la superficie del cuadrado mayor, es equivalente a hallar las superficies de los polígonos que lo forman (dos cuadrados y dos rectángulos) y sumarlas. Luego, las expresiones que representan a las superficies, son equivalentes.
Vamos ahora al cuarto caso: se lo llama cuatrinomio cubo perfecto, que no es otra cosa que, el desarrollo de un binomio elevado al cubo. Posee una deducción similar a las anteriores, sólo que aquí lo que hacemos el buscar las expresiones que permiten hallar el volumen de un cubo. Veamos la imagen:

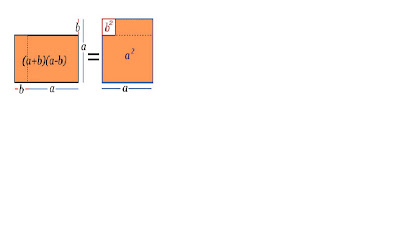
Veamos ahora el quinto caso: se lo llama diferencia de cuadrados. También se puede ver geométricamente, hallando las superficies de estas dos figuras equivalentes:
Ahora que se entiende qué significa, ver en la hoja siguiente, lo que hay que prestar atención para poder factorear una determinada expresión algebraica. Y recuerden, la palabra factorear, proviene de la palabra factor. Un factor, es cada uno de los números o expresiones que intervienen en un producto (multiplicación). Por lo tanto, lo que se busca al factorear un polinomio, es, escribir el mismo polinomio pero en forma de producto. Siendo ambas expresiones equivalentes.

